TRIGONOMETRY

What is Sine,Cosine,Tangent???

Sine,Cosine,Tangent is a basic main function we used in trigonometry and are based on a right-angled triangle.

So,there 3 name to each side of a right triangle helps you to find and calculate sine,cosine and tangent

 

"Opposite" is opposite to the angle θ

"Adjacent" is adjacent (next to) to the angle θ

"Hypotenuse" is the long one

    

So,what is Secant,Cosecant and Cotangent???

Secant,Cosecant and Cotangent is addition to sine,cosine and tangent.There are three other trigonometric function we need to know.These function are simply the reciprocal of sine,cosine and tangent 

Cosecant

Cosecant is the reciprocal of sine. Its formula is:

Secant

Secant is the reciprocal of cosine. Its formula is:

Cotangent

Cotangent is the reciprocal of tangent. Its formula is:

The math will rarely ask you to find the values of these three functions. Most likely, it will ask you to manipulate them in algebraic equations, often with the goal of simplifying the expression down to its simplest form.

                                           Aqil when he was teaching about trigonometric

Example i

Solution

    



Sine and Cosine Graph

In this lesson, you will learn to graph functions of the form y = a sin bx and y = a cos bx where a  and b are positive constants and x is in radian measure.

Amplitude and Period Concept

The amplitude and period of the graph of y = a sin bx and               y = a cos bx are nonzero real numbs, are as follows.

     Amplitude = │a │

Plot of Sine

To sketch the graph of the basic sine and cosine function by hand , it helps to note five key points in one period of each graph : the intercepts, the maximum points and the minimum points. See the figure below :

Plot Of Sine and Cosine

Tangent Graph

The period and vertical asymptotes of the graph of y = a tan bx, where a and b are nonzero real numbers. Are as follows :

Plot of the Tangent Functions

me teaching Trigonometry to Djk1A

Basic Identities

 — Simplify the expression  ( 1 - cos²x )( cosec x )  to a single trigonometric function.

 Solution

   1 -cos^2 x=sin^2 x
        cosec x = 1/sin x

                      =(1-cos^2 x)(cosec x)

                      =(sin^2 x )( 1/sin x )

                      =sin⁡ x

b) secθ x cosθ-cos²θ

Solution

1/cosθ  (cosθ)-cos²θ
1-cos^2 θ=sin²θ

                   =sin²θ

COMPOUND ANGLE

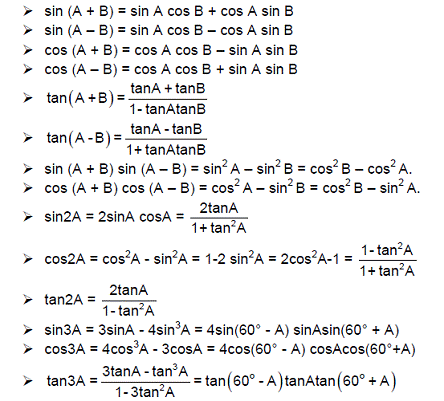
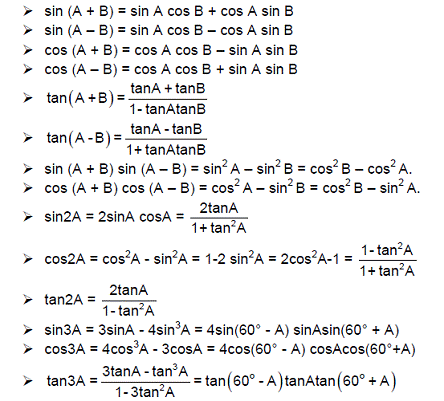
—Simplify the following trigonometric function as a single trigonometric ratio.

a) sin 20˚cos 50˚+cos 20˚sin 50˚

Solution

= sin 20˚cos 50˚+cos 20˚sin 50˚

= sin ⁡(20˚+50˚)

= sin 70˚

b) (tan 53˚+tan 113˚)/(1-tan 53˚tan 113˚)

Solution

=(tan 53˚+tan 113˚)/(1-tan 53˚tan 113˚)

=tan ⁡(53˚+113˚)

=tan 166˚

c) cos53˚ cos32˚ -sin53˚ sin32˚    

Solution   

cos⁡(A+B)= cos53˚ cos32˚-sin53˚sin32˚
                   = cos⁡(53˚+32˚)

             = cos85˚

DOUBLE ANGLE

sin⁡ 2A = 2 sin A cos A)

cos⁡ 2A= cos²A - sin^2 A

           = 1-2 sin^2 A

           =2 cos²A - 1

tan 2A=2 tan A/(1-tan^2 A)

1)Simplify the following trigonometric function as a single trigonometric ratio

a) cos²42˚- sin² 42˚

Solution

   =cos²42˚-sin^2 42˚

   =cos 2 (42˚)

   =cos 84˚

b) (2 tan 68˚)/(1-tan^2 68˚)

Solution

   =(2tan68˚)/(1-tan^2 68˚)

   =tan 2 A

   =tan 2(68˚)

   =tan 136˚

c) 2 cos²x+3 sin x-3=0

  

Solution

  2(1-sin² x)+3 sin x-3=0

     2-2 sin² x+3 sin x-3=0

       -2 sin² x+3 sin x-1=0

        2 sin² x-3 sin x+1=0

      (2 sin x-1)(sin x-1)=0 

     

2 sin x=1                   or         sin x=1

   sin x=1/2               or                x=(sin)^(-1) 1

         x=(sin)^(-1)  1/2

         x=30˚

  

 Q1, x=30˚                           Q1, x=90˚

 Q2, x=180˚-30˚                 Q2, x=180˚-90˚

         x=150˚                               x=90˚

APPLY SINE AND COSINE RULES

STATE THE SINE AND COSINE RULES

What is and cosine rules?

The Sine Rules. The law of Sines (sine rule) is an important rule relating the sides and angles of any triangle (it doesn’t have to be right-angle) : If a,b and c are the lengths of the sides opposite the angles A, B and C in a triangle, then: a = b = c. Sin A sin B Sin C

What is the law of cosines?

Law of Cosines. The law of cosines for calculating one side of a 

Triangle when the angle opposite and the other two sides are known. Can be used in conjunction with the law of sines to find all sides and angle.

SINE:

What are the law of sine?

The law of sines is used to find angles of a general triangle.

If two sides and the enclosed angle to find the third side and 

the other two angles.

What is the formula for sine? 

Sine, Cosine and Tangent are the main function used in 

Trigonometry and are based on a Rigth-angle Triangle.  It 

helps to give a name to each side of a right triangle : 

“Opposite” is opposite to the angle 0 “Adjacent” is adjacent 

(next to) to the angle 0.

Firdaus when he was teaching

CALCULATE THE AREA OF A TRIANGLE  USING THE

FORMULA ½  AB SIN C

Example 1

a) What is the  triangle? Give your answer in space units 

     correct to 1 decimal place.