What is Sine,Cosine,Tangent???
Sine,Cosine,Tangent is a basic main function we used in trigonometry and are based on a right-angled triangle.
So,there 3 name to each side of a right triangle helps you to find and calculate sine,cosine and tangent
"Opposite" is opposite to the angle θ
"Adjacent" is adjacent (next to) to the angle θ
"Hypotenuse" is the long one
So,what is Secant,Cosecant and Cotangent???
Secant,Cosecant and Cotangent is addition to sine,cosine and tangent.There are three other trigonometric function we need to know.These function are simply the reciprocal of sine,cosine and tangent
Cosecant
Cosecant is the reciprocal of sine. Its formula is:
=.gif)
Secant
Secant is the reciprocal of cosine. Its formula is:
=hyp.gif)
Cotangent
Cotangent is the reciprocal of tangent. Its formula is:
.gif)
Solution





Sine and Cosine Graph
In this lesson, you will learn to graph functions of the form y = a sin bx and y = a cos bx where a and b are positive constants and x is in radian measure.
Amplitude and Period Concept
The amplitude and period of the graph of y = a sin bx and y = a cos bx are nonzero real numbs, are as follows.
Amplitude = │a │
Plot of Sine
To sketch the graph of the basic sine and cosine function by hand , it helps to note five key points in one period of each graph : the intercepts, the maximum points and the minimum points. See the figure below :
Plot Of Sine and Cosine
Tangent Graph
The period and vertical asymptotes of the graph of y = a tan bx, where a and b are nonzero real numbers. Are as follows :
Plot of the Tangent Functions
me teaching Trigonometry to Djk1A
Basic Identities

— Simplify the expression ( 1 - cos²x )( cosec x ) to a single trigonometric function.
Solution
1 -cos^2 x=sin^2 x
cosec x = 1/sin x
=(1-cos^2 x)(cosec x)
=(sin^2 x )( 1/sin x )
=sin x
b) secθ x cosθ-cos²θ
Solution
1/cosθ (cosθ)-cos²θ
1-cos^2 θ=sin²θ
1/cosθ (cosθ)-cos²θ
1-cos^2 θ=sin²θ
=sin²θ
COMPOUND ANGLE
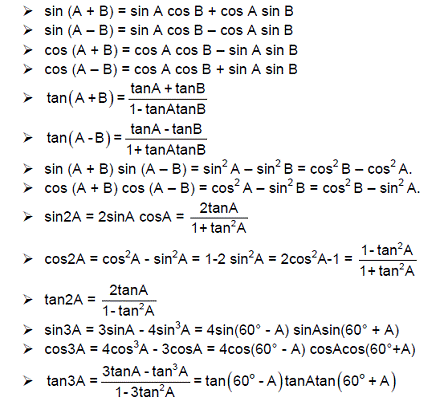
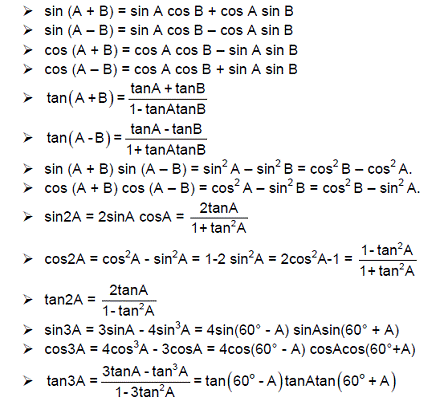
—Simplify the following trigonometric function as a single trigonometric ratio.
a) sin 20˚cos 50˚+cos 20˚sin 50˚
Solution
= sin 20˚cos 50˚+cos 20˚sin 50˚
= sin (20˚+50˚)
= sin 70˚
b) (tan 53˚+tan 113˚)/(1-tan 53˚tan 113˚)
Solution
=(tan 53˚+tan 113˚)/(1-tan 53˚tan 113˚)
=tan (53˚+113˚)
=tan 166˚
c) cos53˚ cos32˚ -sin53˚ sin32˚
Solution
cos(A+B)= cos53˚ cos32˚-sin53˚sin32˚
= cos(53˚+32˚)
DOUBLE ANGLE
c) cos53˚ cos32˚ -sin53˚ sin32˚
Solution
cos(A+B)= cos53˚ cos32˚-sin53˚sin32˚
= cos(53˚+32˚)
= cos85˚
DOUBLE ANGLE
sin 2A = 2 sin A cos A)
cos 2A= cos²A - sin^2 A
= 1-2 sin^2 A
=2 cos²A - 1
tan 2A=2 tan A/(1-tan^2 A)
1)Simplify the following trigonometric function as a single trigonometric ratio
a) cos²42˚- sin² 42˚
Solution
=cos²42˚-sin^2 42˚
=cos 2 (42˚)
=cos 84˚
b) (2 tan 68˚)/(1-tan^2 68˚)
Solution
=(2tan68˚)/(1-tan^2 68˚)
=tan 2 A
=tan 2(68˚)
=tan 136˚
c) 2 cos²x+3 sin x-3=0
Solution
2(1-sin² x)+3 sin x-3=0
2-2 sin² x+3 sin x-3=0
-2 sin² x+3 sin x-1=0
2 sin² x-3 sin x+1=0
(2 sin x-1)(sin x-1)=0
2 sin x=1 or sin x=1
sin x=1/2 or x=(sin)^(-1) 1
x=(sin)^(-1) 1/2
x=30˚
Q1, x=30˚ Q1, x=90˚
Q2, x=180˚-30˚ Q2, x=180˚-90˚
x=150˚ x=90˚
APPLY SINE AND COSINE RULES
STATE THE SINE AND COSINE RULES
What is and cosine rules?
The Sine Rules. The law of Sines (sine rule) is an important rule relating the sides and angles of any triangle (it doesn’t have to be right-angle) : If a,b and c are the lengths of the sides opposite the angles A, B and C in a triangle, then: a = b = c. Sin A sin B Sin C
What is the law of cosines?
Law of Cosines. The law of cosines for calculating one side of a
Triangle when the angle opposite and the other two sides are known. Can be used in conjunction with the law of sines to find all sides and angle.
SINE:
What are the law of sine?
The law of sines is used to find angles of a general triangle.
If two sides and the enclosed angle to find the third side and
the other two angles.
What is the formula for sine?
Sine, Cosine and Tangent are the main function used in
Trigonometry and are based on a Rigth-angle Triangle. It
helps to give a name to each side of a right triangle :
“Opposite” is opposite to the angle 0 “Adjacent” is adjacent
(next to) to the angle 0.
Firdaus when he was teaching
CALCULATE THE AREA OF A TRIANGLE USING THE
FORMULA ½ AB SIN C
Example 1

























